Solving the Mountain Bike problem
In 2019, I was trying to get an interview at redmark.com, they were publishing this mountain biking/skiing problem as a CV screening challenge. At that time, I tried to solve it but unfortunately, I couldn’t crack it by myself. Then recently I got an interview with a fintech startup, before the interview, they asked me to complete the same Redmark’s challenge but they rename it “mountain biking”.
This time, I told myself: “I have to solve it now or this challenge will come back to me again and again in future if I don’t solve it” :) I didn’t crack it on time for an interview because of short timing, but I spent the next Saturday solving it and code it as a serious way of working task.
So here we go, below is the original problem statement:
At company XXX, we always like to have some challenges and solve small fun problems, here is one that we enjoyed recently. You take a look at the map of the mountain and try to find the longest path down. In digital form, the map will be in a .txt file and will look like the grid below.
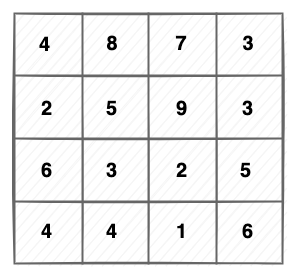
4 4
4 8 7 3
2 5 9 3
6 3 2 5
4 4 1 6
The first line (4 4) indicates that this is a 4x4 map. Each number represents the elevation of that area of the mountain. From each position in the grid, you can go north, south, east, west - but only if the elevation of the area you are going into is less than the one you are in. (i.e. you can only cycle downhill). You can start from anywhere on the map and look for a starting point with the longest possible path down as measured by the number of positions you visit. If there are several paths of the same length, you want to take the steepest (i.e. the largest difference between your starting elevation and your ending elevation).On this particular map, the longest path has a length of 5:
[ 9, 5, 3, 2, 1 ]There is another path with a length of 5:
[ 8, 5, 3, 2, 1 ].However, the tie is broken by the first path being steeper, dropping from 9 to 1 (a drop of 8), rather than just 8 to 1 (a drop of 7). Your challenge is to write a program in Java to find the longest and then the steepest path on this map specified in the format above. Its max size is 1000x1000, and all the numbers on it are between 0 and 1500.
The first thing that came into my mind is “Let’s google it” and find the solution, after doing few searches, it was easy to find out a few solutions, some solution code are Javascript based, some Python and Java ones. You may think that why I do Google searching if I want to solve this problem? The answer of it is my habit of thinking after more than 10 years in this industry. When you have a problem, you should always try to find the available solutions firstly, rather than re-inventing the wheel. For me, I shall try to understand the solution and optimize or adjust them according to my specific use cases. Unfortunately, This time, I can’t understand any of available solution, that means I have to solve it by myself.
This is my Top-down thinking approach to solve it. Starting I draw the martrix on my blank paper,
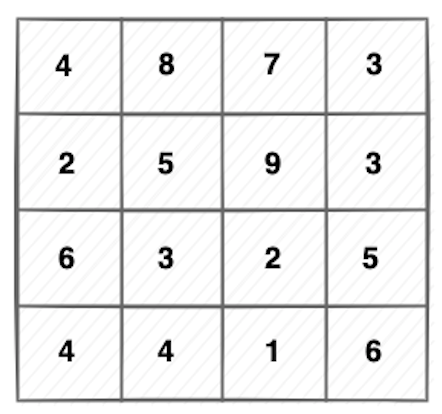
Because we are finding the longest path, so I think it makes sense to say: a first node (mountain) of the longest path has to be the biggest node. So we can pick (9), and from (9) we are able to go (5), (7), (3), (2).
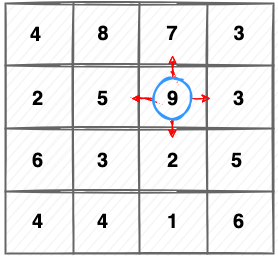
Now, let try to move to (5), then we see how it is going to. But from (5), again we have to decide if we want to follow (2) or we want to follow (3):
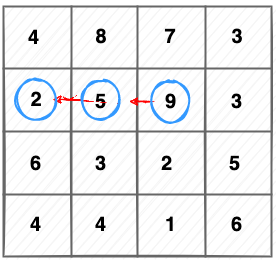 or
or 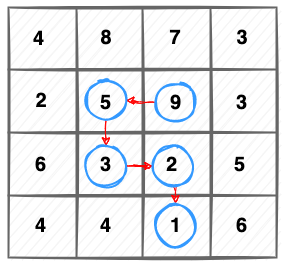
When we are at (2), it is a dead-end for our journey, so we shall follow (3). We easily realize that is the only way to move forward is (2) -> (1).
Finally we can conclude ourself that if we start from mountain (9) and we go to (5) we have two paths:
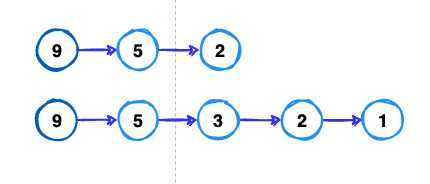
Now, let us try again, this time, from (9) we don’t go to (5) but we go to (7) so we will have another path:
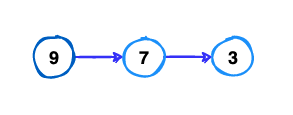
Repeating the same steps again and again, we shall have more below paths:
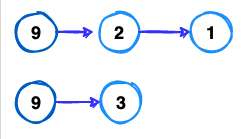
Finally we have the longest path which starts from mountain (9) is:
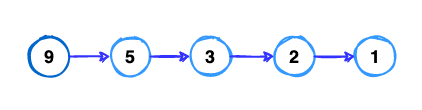
Hmmm… we shall ask ourselves if the longest path starts from the highest mountain? Of course, it is not true, what happens if we start from 8, it is possible to have a longer path than the above one.
But we don’t make ourself fool, we shall do testing using above approach, we start from point (8). If we don’t make any mistake, the longest path which starts from (8) is
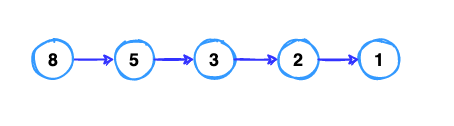
At this point, we have our first conclusion is the longest path can start from any mountain in the matrix. So we need to try from all mountains.
The second conclusion, you easily realize the matrix are multiple of directed acyclic graphs
 vs
vs
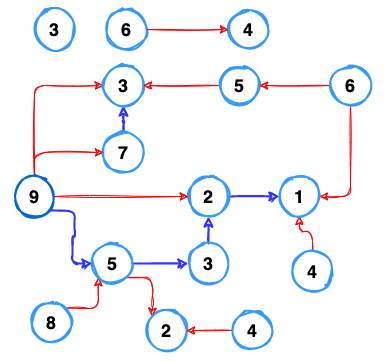
The original challenge’s statement becomes “Find the longest path in a directed acyclic graph (DAG)”. Ok, let forget about the complexity of this problem. We travel back to our university time, visit our old school and try to learn again “how to find the longest path from a root node in a simple below DAG”
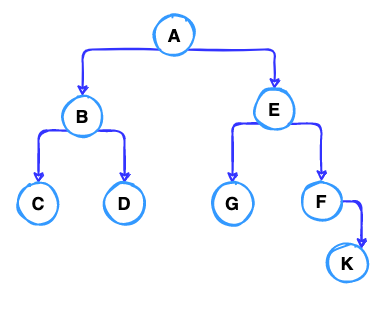
Knowledge from our old-time class, to find the longest path, we normally use algorithms Depth First Search (DFS) to find all possible paths from node (A) and then, in the end, we choose the longest path in a result list.
DFS will provide us a result list below:
(A) -> (B) -> (C)
(A) -> (B) -> (D)
(A) -> (E) -> (G)
(A) -> (E) -> (F) -> (K)
So the longest path is: (A) -> (E) ->(F) -> (K)
Conclusion:
We apply the same approach to the mountain bike problem, we traverse all nodes/mountains, using DFS find the longest path, then we will have a set of longest paths from all points/mountains. Next is simply choosing the longest path from a list of longest paths.
Ok, I am talking too much! we code the solution then, the full code you can download from the GitHub link: https://github.com/cseblog/mountainbike
I walk you through a journey that I code this project
Step 1: Of course we create a Node class. A node will have friend nodes, from that we can visit our friends if needed. In this challenge, each Node will have a maximum of 4 friends which are Up Node, Down Node, Left Node, Right Node. Like people, some unlucky Nodes don’t even have any friends such as Node (3). Or some are born unfortunately on the edge of matrix life so they will have few friends. That is how the function addFriends() is working.
package com.jajudev.mountainbike.model;
import lombok.Data;
import lombok.Getter;
import lombok.Setter;
import java.util.ArrayList;
import java.util.List;
@Setter
@Getter
public class Node {
int v;
List<Node> friends;
public Node(int value) {
v = value;
friends = new ArrayList<>();
}
public void addFriends(int s, Node[][] matrix, int i, int j) {
int[] up = new int[]{i - 1, j};
int[] down = new int[]{i + 1, j};
int[] left = new int[]{i, j - 1};
int[] right = new int[]{i, j + 1};
if (up[0] >= 0 && v > matrix[up[0]][up[1]].getV()) {
friends.add(matrix[up[0]][up[1]]);
}
if (down[0] < s && v > matrix[down[0]][down[1]].getV()) {
friends.add(matrix[down[0]][down[1]]);
}
if (left[1] >= 0 && v > matrix[left[0]][left[1]].getV()) {
friends.add(matrix[left[0]][left[1]]);
}
if (right[1] < s && v > matrix[right[0]][right[1]].getV()) {
friends.add(matrix[right[0]][right[1]]);
}
}
@Override
public String toString() {
return "" + v;
}
}
Step 2: We need to convert the input matrix to a graph. The Graph class have a build() function to convert the matrix string to a list of adjective: List
package com.jajudev.mountainbike.model;
import lombok.NoArgsConstructor;
import lombok.extern.slf4j.Slf4j;
import java.util.ArrayList;
import java.util.List;
import java.util.stream.Stream;
@Slf4j
@NoArgsConstructor
public class Graph {
int size;
List<Node> nodes = new ArrayList<>();
/**
* Build graph from a string of matrix
* Ex: "4 8 7 3 2 5 9 3 6 3 2 5 4 4 1 6"
* @param n
* @param matrixStr
*/
public void build(int n, String matrixStr) {
String[] strArr = matrixStr.split(" ");
int[] intArr = Stream.of(strArr).mapToInt(Integer::parseInt).toArray();
build(n, intArr);
}
public void build(int s, int[] arr) {
Node[][] matrix = new Node[s][s];
for (int i = 0; i < s; i++) {
for (int j = 0; j < s; j++) {
matrix[i][j] = new Node(arr[i * s + j]);
}
}
for (int i = 0; i < s; i++) {
for (int j = 0; j < s; j++) {
Node node = matrix[i][j];
node.addFriends(s, matrix, i, j);
nodes.add(node);
}
}
}
public void print() {
nodes.forEach(n -> {
List<Node> friends = n.getFriends();
List<Integer> friendList = new ArrayList<>();
friends.forEach(f -> friendList.add(f.getV()));
log.info("{}-> {}", n.getV(), friendList);
});
}
public Path getLongestPath() {
List<Path> paths = new ArrayList<>();
this.nodes.stream().forEach(n -> {
Path friendLongestPath = this.getLongestPathByNode(n);
paths.add(friendLongestPath);
});
Path longestPath = new Path();
for (int i = 0; i < paths.size(); i++) {
Path currPath = paths.get(i);
if (currPath.compare(longestPath) ) {
longestPath = currPath;
}
}
return longestPath;
}
public Path getLongestPathByNode(Node n) {
Path path = new Path();
path.add(n);
List<Node> friends = n.getFriends();
Path maxPath = null;
for (int i = 0; i < friends.size(); i++) {
Path currentPath = getLongestPathByNode(friends.get(i));
if (currentPath.compare(maxPath)) {
maxPath = currentPath;
}
}
if (maxPath != null) {
path.addAll(maxPath);
}
return path;
}
}
The graph also has two functions that implement a recursive DFS to get the longest path from one matrix point, the below function will travel from a Root node, return the longest path.
public Path getLongestPathByNode(Node n)
But our customers can be skiing or biking from any mountain, so we shall try to get the longest path from all mountains. We assume there is a dump fat biker who just wants to bike from the lowest mountain also. No choice, that is how the people are.
public Path getLongestPath()
Step 3: You are noticing that I mention a lot of word “Path” in my blog, ahh yes we shall create a Path class, this class simply holds a list of node belongs to a path, and also provide a method to compare two paths.
package com.jajudev.mountainbike.model;
import lombok.Getter;
import lombok.Setter;
import java.util.ArrayList;
import java.util.List;
@Getter
@Setter
public class Path {
List<Node> nodeList;
public Path(){
nodeList = new ArrayList<>();
}
public void add(Node node){
nodeList.add(node);
}
public void addAll(Path path){
this.nodeList.addAll(path.getNodeList());
}
public int getSize(){
if(nodeList.isEmpty() || nodeList == null){
return 0;
}
return nodeList.size();
}
public boolean compare(Path p) {
if(p == null){
return true;
}
List<Node> l = p.getNodeList();
if (nodeList.size() > l.size()) {
return true;
}
if (nodeList.size() < l.size()) {
return false;
}
//If the sizes of paths are equal, we will consider
//the delta difference between
//first node and last node.
if( nodeList.size() == l.size()) {
int delta1 = nodeList.get(0).getV() - nodeList.get(nodeList.size() -1).getV();
int delta2 = l.get(0).getV() - l.get(l.size() -1).getV();
if(delta1 >= delta2){
return true;
} else {
return false;
}
}
return true;
}
}
Assuming the DAG or the matrix have N x N nodes, the complexity of DFS from one node is BigO(N). So the complexity for finding the longest path is BigO(N^2),we also cost BigO(N^2) to build the graph, in the end, the overall time complexity (including building graph + finding a longest path) is BigO(N^2) + BigO(N^2) = BigO(N^2). I believe it is not the best solution out there, but it is a working solution. I’m a bit happy now. There is one thing I don’t mention is testing. Of course, to solve a problem we can’t ignore the test. So I try to add Unit tests along the way I am developing all classes. One test case is for small test data, and another is for reading a 1000x1000 matrix file.
package com.jajudev.mountainbike.model;
import lombok.extern.slf4j.Slf4j;
import org.junit.Before;
import org.junit.Test;
import java.io.IOException;
import java.util.ArrayList;
import java.util.List;
@Slf4j
public class GraphTest {
Graph graph = new Graph();
@Before
public void setUp() throws Exception {
}
@Test
public void test1() {
graph.build(4, "4 8 7 3 2 5 9 3 6 3 2 5 4 4 1 6");
// graph.print();
Path maxChain = graph.getLongestPath();
log.info("Final longest path: {}", maxChain.getNodeList());
//TODO: Assert here
}
@Test
public void test2() throws IOException {
String data = new String(getClass()
.getClassLoader().getResourceAsStream("test2.txt").readAllBytes());
String[] dataArr = data.split("\n");
int size = Integer.parseInt(dataArr[0].split(" ")[0]);
String matrix = "";
for (int i = 1; i < dataArr.length; i++) {
matrix = String.format("%s %s", matrix, dataArr[i]);
}
graph.build(size,matrix.trim());
Path maxChain = graph.getLongestPath();
log.info("Final longest path: {}", maxChain.getNodeList());
//TODO: Assert here
}
}
Thank you for reading. By applying this thinking we can solve a lot of similar challeges. For example, below are two more interesting challeges for you to practise.
Example 1:
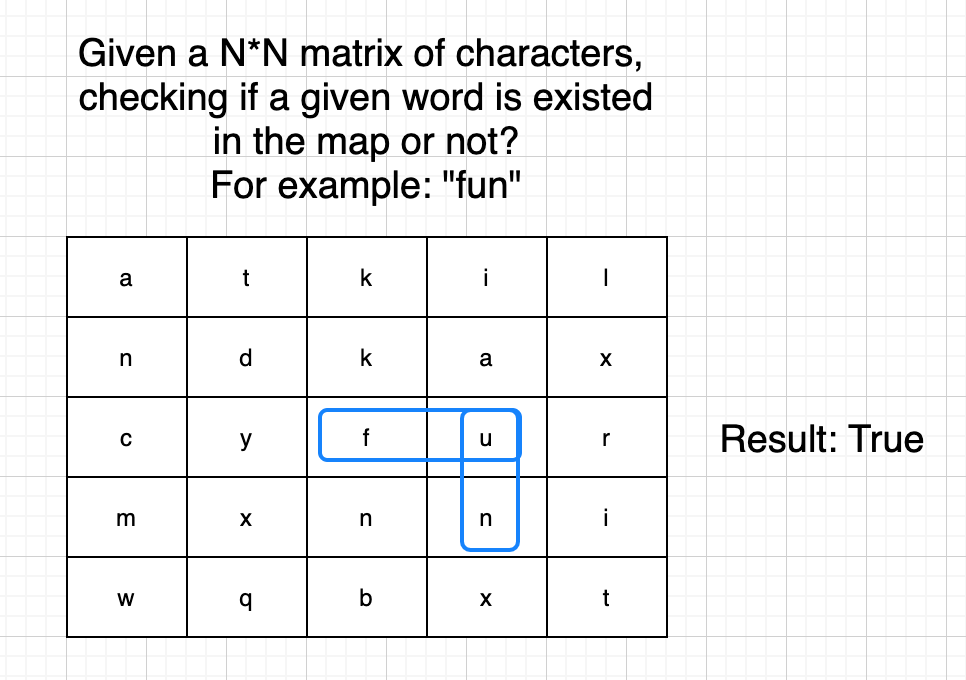
Example 2